Contoh Pertanyaannya:
Sumber : Rumus-mtk.blogspot.com
Mister Rumus MTK, bagaimana sih menentukan akar pangkat tiga sebuah bilangan itu? Misalnya bagaimana menentukan nilai dari
Mencari nilai dari ![\sqrt[3]{100} \sqrt[3]{100}](http://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B100%7D&bg=ffffff&fg=333333&s=0) , secara geometris, berarti menentukan panjang rusuk sebuah kubus yang volumnya adalah
, secara geometris, berarti menentukan panjang rusuk sebuah kubus yang volumnya adalah  satuan volum. Dengan menggunakan sedikit kemampuan menaksir (memperkirakan), maka dengan mudah kita dapatkan bahwa perkiraan panjang rusuk sebuah kubus–yang mempunyai volum 100 satuan volum– adalah 4, 64… satuan panjang. Sehingga, kita bisa menyimpulkan bahwa nilai dari
satuan volum. Dengan menggunakan sedikit kemampuan menaksir (memperkirakan), maka dengan mudah kita dapatkan bahwa perkiraan panjang rusuk sebuah kubus–yang mempunyai volum 100 satuan volum– adalah 4, 64… satuan panjang. Sehingga, kita bisa menyimpulkan bahwa nilai dari ![\sqrt[3]{100} \sqrt[3]{100}](http://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B100%7D&bg=ffffff&fg=333333&s=0) kira-kira adalah 4, 64….
kira-kira adalah 4, 64….
Cara lain untuk mempermudah dalam menentukan akar pangkat tiga sebuah bilangan adalah dengan menggunakan bantuan sifat-sifat logaritma–dipelajari di tingkat SMA (Sekolah Menengah Atas). Untuk kasus di atas, dalam menentukan ![\sqrt[3]{100} \sqrt[3]{100}](http://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B100%7D&bg=ffffff&fg=333333&s=0) adalah sebagai berikut.
adalah sebagai berikut.
Misalkan ![x = \sqrt[3]{100} x = \sqrt[3]{100}](http://s0.wp.com/latex.php?latex=x+%3D+%5Csqrt%5B3%5D%7B100%7D&bg=ffffff&fg=333333&s=0) , maka dengan menggunakan sifat-sifat logaritma, kita bisa menulis seperti berikut ini:
, maka dengan menggunakan sifat-sifat logaritma, kita bisa menulis seperti berikut ini:
log 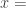 log
log ![\sqrt[3]{100} \sqrt[3]{100}](http://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B100%7D&bg=ffffff&fg=333333&s=0)
log 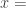 log
log 
log 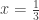 log
log 
log 
log 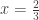
log 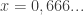
Dengan menggunakan tabel logaritma, anti logaritma dari log 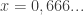 kira-kira adalah
kira-kira adalah  . Dengan demikian,
. Dengan demikian, ![x = \sqrt[3]{100} = 4, 642 x = \sqrt[3]{100} = 4, 642](http://s0.wp.com/latex.php?latex=x+%3D+%5Csqrt%5B3%5D%7B100%7D+%3D+4%2C+642&bg=ffffff&fg=333333&s=0) .
.
Nah, untuk kasus yang lain dapat ditangani dengan cara yang serupa dengan memanfaatkan sifat-sifat logaritma. Dengan menggunakan cara serupa di atas (menggunakan sifat-sifat logaritma), kita pun dapat menentukan akar pangkat ke-n dari suatu bilangan.
Bagi Anda yang kesulitan mengikuti proses penentuan akar pangkat tiga–dengan menggunakan sifat-sifat logaritma, saya mohon maaf, karena salah satu caranya memang begitu yakni: menggunakan sifat-sifat logaritma yang dipelajari di tingkat SMA.
Sumber : Rumus-mtk.blogspot.com












.png)



